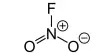
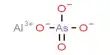
Application of Centripetal and Centrifugal Force: Motion of a cyclist along a curved path:
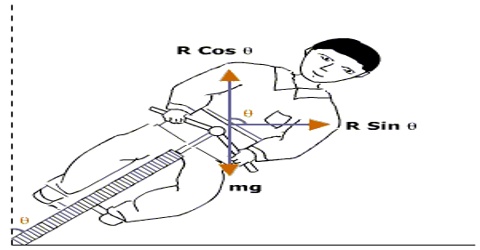
During turning the cyclist automatically inclines toward inside i.e., towards the centre of the turning of the road (figure). As a result, the cyclist asserts pressure on the road inclinedly, so the reaction R of the road acts making an angle θ with the horizontal. The horizontal components, the reaction provides the necessary centripetal force. If the cyclist along with the cycle bends inside making an angle θ with the vertical in order to balance in the turning then the vertical and horizontal components of the reaction R will be F cos θ and F sin θ respectively. This vertical component of reaction balances the weight mg of the cyclist along with the cycle and the horizontal component provides the necessary centripetal force, mv2/r.
R cos θ = mg
and, R sin θ = mv2/r.
or, tan θ = v2/rg
then, θ = tan-1 (v2/rg)
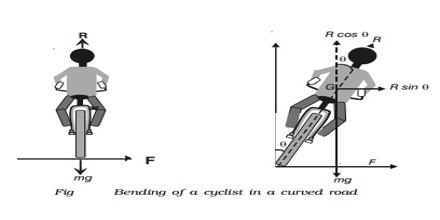
The cyclist along with the cycle is to take turn making this angle θ. The larger the speed of the cyclist, less will be the radius of the turning and he will have to bend more.
From the above equation velocity of the cyclist along with the cycle, v = √(rg/tanθ) can be determined.