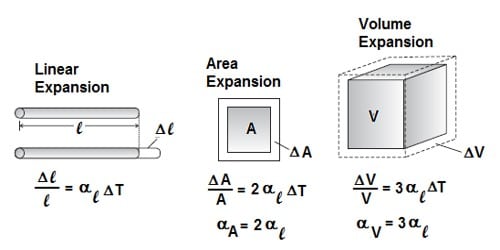
The area of a solid is increased with an increase of temperature. It is called superficial expansion. Whenever there is an increase in the size of a body due to heating, then the body is said to be expanded and the fact is known as expansion.
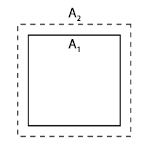
Let the initial surface area of a solid at θ1 temperature = A1
When the temperature is increased to θ2 the final surface area =A2
So, Increase in temperature = θ2 – θ1
And the increase in area = A2 – A1
The coefficient of superficial expansion is expressed by the symbol β (beta). The amount by which unit area of a material increases when the temperature is raised by one degree is called the coefficient of superficial (i.e. area) expansion and is represented by β (Greek beta).
Superficial expansion, β = [(A2 – A1) / A1(θ2 – θ1)] ….. ………. ………(1)
[Increase in surface area / (Initial area x increase of temperature)]
In equation (1) if the surface area, A1 = 1 m2 and the increase of temperature (θ2 – θ1) = 1K is considered, then the increase in surface area, β (beta) = A2 – A1 = increase in surface area. If the temperature increases, then the volume of the substance also increases. Usually, this is known as thermal expansion.
Superficial Expansion of Solids: The coefficient of superficial expansion is defined as the ratio of increase in area to its original area for every degree increase in temperature.
Coefficient of superficial expansion = Increase in area / (Initial area – Rise in temp) (°C) = 2 × coefficients of linear expansion.
So, the increase in surface area of 1 m2 surface area of a solid for the rise of temperature 1K is called the coefficient of superficial expansion of the material of that solid. In case of expansion of a solid, normally linear expansion coefficient is generally employed. Its unit is K-1. The coefficient of superficial expansion of copper is 33.4 x 10-6 K-1. We can express it in this method that it is the fractional change in length or volume per unit change in temperature. It means that if the temperature of a copper body is increased through 1K, then the increase in surface area of copper is 33.4 x 10-6 m2.