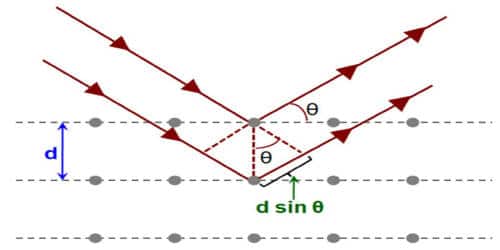
The significance of Bragg’s law in electron diffraction and microscopy is then discussed, with particular emphasis on differences between X-ray and electron diffraction. Bragg’s law and the electron microscope imaging of lattice planes in crystals. Bragg’s real-space vision was that X-rays are reflected from lattice planes in crystals
The significance of Bragg’s equation
(1) If we use X-rays of known wavelength (λ), then the interatomic distance (d) in an unknown crystal can be calculated. On the other hand, if we use a crystal whose interatomic distance ‘d’ is known, then the wavelength of X-rays can be calculated. In electron microscopy, the electron wavefunction in the image plane is the FT of that in the diffraction plane, which is the FT of the wavefunction on the exit surface of the crystal.
(2) Bragg’s equation gives the essential condition for diffraction to occur. Hence, the electron microscope image of a crystal directly reveals the Bragg planes used for the imaging process
(3) When the experiment is done, there will be a maximum reflection at a particular angle θ. That angle is noted. It corresponds to first-order reflection (n=1). If the angle ‘θ’ is increased, maximum reflection occurs at some other higher angle. It corresponds to second-order reflection (n=2). Similarly, the third, fourth and higher order of reflection occurs at certain specific angles.
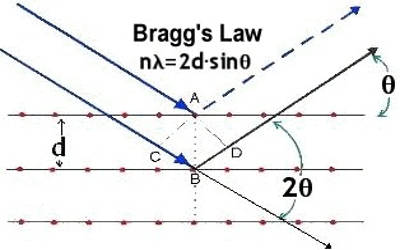
The values of angles obtained are in accordance with the Bragg’s equation. Hence Bragg’s equation is experimentally verified. As an example of such differences, the critical voltage effect in electron diffraction is described. It is then shown that the lattice imaging of crystals in high-resolution electron microscopy directly reveals the Bragg planes used for the imaging process, exactly as visualized by Bragg in his real-space law.
The significance of Bragg’s law in electron diffraction and microscopy is then discussed, with particular emphasis on differences between X-ray and electron diffraction. As an example of such differences, the critical voltage effect in electron diffraction is described. It is then shown that the lattice imaging of crystals in high-resolution electron microscopy directly reveals the Bragg planes used for the imaging process, exactly as visualized by Bragg in his real-space law.