Elastic Potential Energy

Elastic Potential Energy

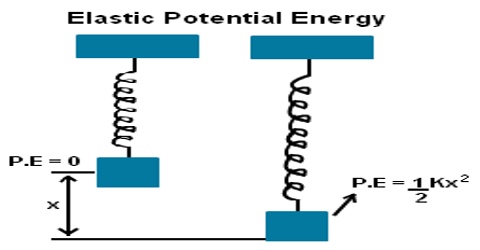
Within elastic limit, if a force is applied on a body it becomes strained and when the force is withdrawn the body gets back its original shape. In order to strain or deform a body, we need to do work on the body. This work remains stored as potential energy. This energy is called elastic potential energy. Elastic potential energy is energy stored as a result of applying a force to deform an elastic object. Let find the equation of elastic potential energy.

The potential energy of a stretched spring

Let one end of an ideal horizontal spring be fixed at a wall and a block of mass m is attached to the other end. The block can move on a frictionless horizontal surface (Figure). We neglect the mass of the spring compared to the mass of the block.

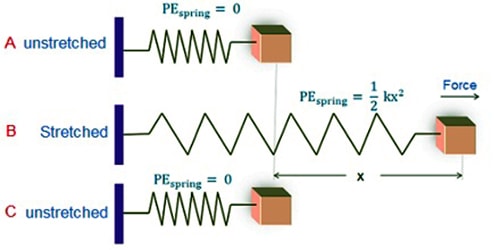
Fig: Elastic Potential Energy

Now, the spring is stretched along its length by a distance x. Due to elastic property, the spring will exert a force called restoring force which will try to oppose the deformation. This restoring force is proportional to the displacement and acts opposite to the displacement i.e.,

F ∞ – k

or, F = kx.

where k is a constant of proportionality and is called force constant of the spring. Now, to stretch the spring we must do work by applying a force F’ equal but opposite to the force F exerted by the spring. So,

Now, to stretch the spring we must do work by applying a force F’ equal but opposite to the force F exerted by the spring. So,

F’ = – F = – (- kx) = kx

This work remains stored as potential energy in the spring. So, potential energy;

U = W = ^x∫₀ Fdx = ^x∫₀ kx dx

= k ^x∫₀ x dx = k [x²/2]^x₀

so, U = ½ kx²

While compressing the spring by x, the same amount of energy will remain stored as potential energy in the spring.