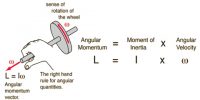
Gravitational force between the earth and the moon:
The moon rotates in a circular orbit around the earth. In the Solar System, for example, if you know the period and the radius of one planet orbit, by knowing another planet’s period you can determine its orbit radius.
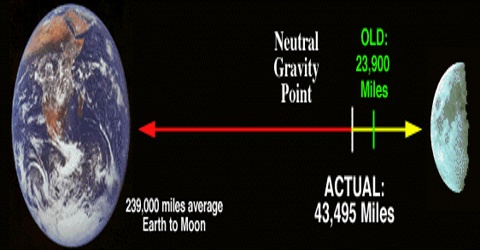
We know, Radius of this circle is 3.84 x 1010 cm. So, distance of the moon from the earth, d = 3.84 x 1010 cm = 3.84 x 108 m.
We know, mass of the earth, M1 = 5.96 x 1027 g = 5.96 x 1024 kg
Mass of the moon, M2 = 7.33 x 1025 g = 7.33 x 1022 kg
So, force acting between the earth and the moon is, F = [Gm1m2/d2]
The Moon has roughly 1/4 the Earth diameter so it experiences 1/4 the tidal force (27% actually)
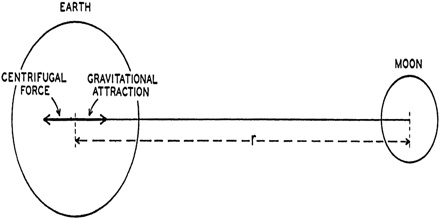
G = universal gravitational constant
M = mass of the Earth
m = mass of the Moon
d = center-to-center Earth Moon distance
= (6.67 x 10-11) x [(5.96 x 1024) x (7.33 x 1022)] / (3.84 x 108)2
= 1.946 x 1020 N
Gravitational force acting between the sun and the earth is 175 times more than the gravitational force acting between the earth and the moon. Due to the influence of gravitational force acting between the sun and the earth and between the earth and the moon there occurs high tide and low tide.